Thinking Mindset: Advancing Analytics
"Mindset" is the latest celebrity buzzword in academia, particularly when it comes to the educational frontiers of ability and learning. The intuitive polarisation between having a "growth" mindset (a belief that abilities are malleable and can be progressively honed), versus a "fixed" mindset (a belief that abilities are immutable), may seem like the beginning of a "there are two types of people" meme, but does have very real ramifications for educational attainment. Because of the conceptual ease and parsimonious costs, interventions to promote growth mindsets in students and teachers have been trialled across the education spectrum, from secondary schools in Peru by the Oxford-affiliated RISE Programme (2017), to the UK Office for Students funded 'Changing Mindsets' project within higher education (2018).
Professor Carol Dweck is often heralded as the 'mother of mindset', though she herself spares no efforts to remind purveyors of the mindset approach that the uplifted students are the real champions. That being said, there is some briar beneath the brain; prickly challenges to the true efficacy of a growth mindset that have the potential to incite discord of the magnitude of the 1990s meta-analysis skirmish between Ryan & Deci and Cameron & Pierce. This has been defused to some extent by Dweck & Yeager's (2019) tasteful genealogy of mindset, which at the same time provides a reflection of its culmination over the past 35 years, with an invitation to "bridge" its eras of development. It is through this invitation that I attempt to dust off the covers of the pre-empirical, analytic approach to psychology, and bring mindset into a 3rd dimension.
It must be remembered that psychological mechanisms do not generally account for much of the variance in individual behaviour compared to those theorised say, in the medical sciences, and even where they might, the vagueness of definitional boundaries adds to their complexity. Because of this, earlier lightweight, algebraically-driven formulations have been usurped by statistical techniques and structural equation modelling which tend to be more flexible toward the proliferation of constructs, at the cost of balancing validity and reliability. The purpose of this thought segment is to demonstrate how an analytic approach can still add value in parallel to empirical research, exemplified using the case of mindsets.
Given the natural links between mindset and motivation, an obvious place to start would be Atkinson's (1957) theory of achievement motivation for uncertain or "risky" tasks, which was a seminal and widely debated piece in the 1960s and 70s, and is still regarded as foundational study today. Atkinson's original contribution postulated the resultant tendency to achieve a goal, Tach, as:

where:
-
Ms and Mf are the strengths of arousal or tendency to approach success and avoid failure, respectively.
-
Is and If are the incentives (for now considered to be intrinsic) to succeed at the goal and to avoid failure, respectively.
-
Ps and Pf are the expectancies, or more precisely, probabilities of achieving and failing at the goal, respectively. These are mutually exclusive and sum to 1.
This is perhaps one of the progenitors of contemporary expectancy-value theories of motivation, and it also claims the benefit of an explicit specification for approach-avoidance channels. In Atkinson's paper, additional postulates on the relationship between incentives and expectancies lead to a highly tractable U-shaped quadratic function for achievement motivation in terms of the probability of success, as shown in Figure 1. I have tweaked the x-axis dimension in terms of the relative difficulty of the task instead of the probability of success, by invoking a random variable 'Attempt', which is uniformly distributed on [0,1] such that:
Prob(Success) = Prob(Attempt ≥ Difficulty│Effort)
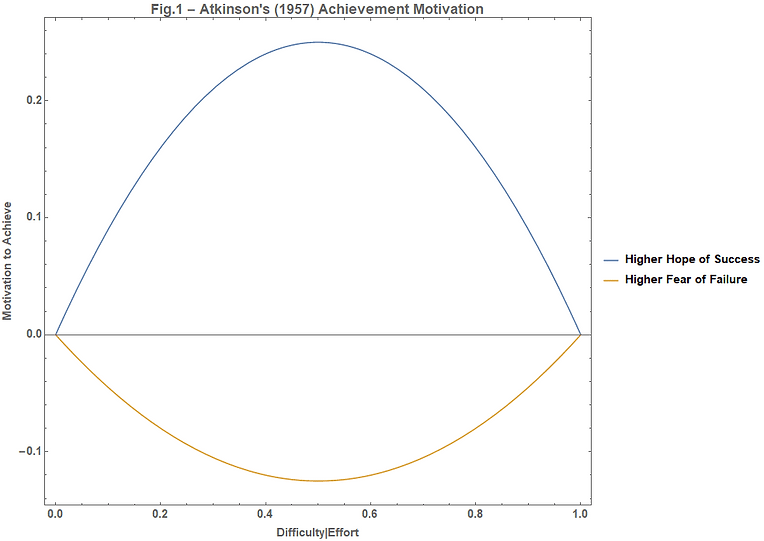
Switching from probabilities to Difficulty on the independent axis is a trivial manoeuvre that transposes the curve orientation, but is an important step for the mindset analysis. Crucially, it preserves the U-shaped characteristic, which nicely models the empirical result that people with higher hope of success (Ms > Mf) prefer tasks of average difficulty, while those with higher fear of failure (Mf > Ms) prefer very easy or very difficult ones. We can also glean from this interpretation how motivational tendencies might be related to Vygotsky's popular Zone of Proximal Development concept in learning (ZPD), which can be considered as the optimal difficulty range corresponding to the achievement motivation above some threshold limit.
Subsequent research which investigated the predictive value of Atkinson's model found that the quadratic reduction may be too rigid a constraint (eg. Revelle & Michaels (1976) which considers the implications of task repetition). To circumvent this, Merrick (2016, pg. 27) generalises the algebra so that the basic U-shape is intact, but is more parametrically flexible with respect to the slopes, ZPD location, and turning point. The U is broken into two 'arms', each of which specifies either the approach or avoidance channel, and is a sigmoid function of the form:

where:
-
Sach is the strength of the tendency to approach or avoid (the height of the arm)
-
ρach is the gradient of success approach or failure avoidance (the slope of the arm)
-
Mach is the turning point of success approach or failure avoidance (the location of the maximum, minimum or inflection)
-
D│E is the task difficulty relative to effort (equivalently 1-D│E is the probability of success)
This allows for individual differences in achievement motivation to be modelled with much greater flexibility as in Figure 2.

The question now, is how can we account for the presumed effects of ability and mindset? To start with, we can assume that the task difficulty relative to effort is a distinct concept from the task difficulty relative to ability. This allows us to simply extend the resultant motivation curve in Figure 2 into 3D space, with Difficulty│Ability as the new independent dimension, as shown in Figure 3.

We can now try to understand how empirically determined characteristics of a fixed mindset would be emulated in this space. Consider firstly the relationship between our effort beliefs and notions of ability. It is widely recognised in the academic literature that people with a fixed mindset tend to associate trying hard with a lack of ability, eg. Haimovitz & Dweck (2017). This effectively suggests a negative correlation between the difficulty relative to ability and the effort-based ZPD. I have introduced this parametrically as a 'twist' in the shape of the curve along the Difficulty│Ability axis (Figure 4).

The final aspect of a fixed mindset to account for is the immutability of ability relative to effort, which is paramount in behavioural explanations provided by Weiner's (1972) review on attribution theories of motivation. If difficulty relative to ability is essentialised as a constraint, the height of the resultant motivation function should decrease gradually toward zero, if difficulty relative to effort is held constant. The amalgamation of these parametric elements of a fixed mindset is represented in the dynamic Figure 5.
Fig. 5 -Sigmoid Achievement Motivation under Fixed Mindset - Ability as a Constraint
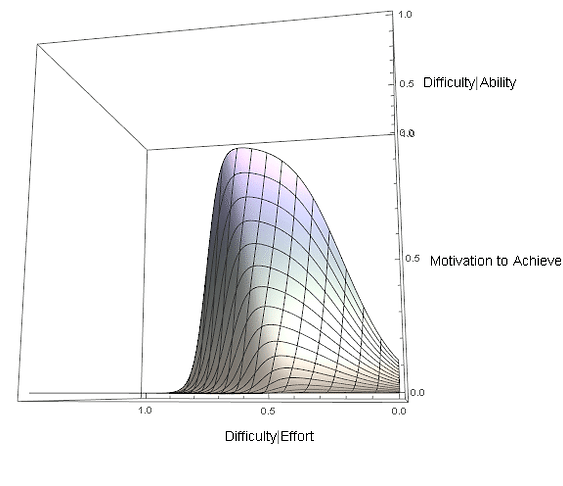
This waffle-cone profile of achievement motivation under a fixed mindset seems reasonable, and is consistent with the main empirical outcomes in the relevant literature. There is sufficient parametric flexibility in the model to account for some individual variation - we can imagine bending or shifting the cone in various ways. But the acid test now is whether we can understand how adapting a growth mindset would influence this profile?
Certainly, a growth mindset can change the relative impact of the avoidance channel for performance-oriented people. We can account for this in the model using parameters which adjust the open end of the cone, that is, those which influence the ZPD in Figure 2.
Secondly, a growth mindset can influence the 'twist' - the negative correlation between effort beliefs and perceptions of ability which affect the difficulty levels we are prepared to undertake. Again, this is straightforward enough to model by adjusting the same parameters as in Figure 4.
The final major impact of growth mindset is also the trickiest to model - that related to its malleability and how it is associated with attribution beliefs for success or failure. In Figure 5, ability is treated as a constraint which is progressively undermined the more difficult the task. It seems reasonable that the alternative condition under a growth mindset would be to treat ability as a resource similar to effort; one that can be mustered and shaped but which also has to be incentivised in its own right.
The way we can incorporate this characteristic is also straightforward. The property of ability as a resource is automatically induced in the motivation profile when we think about the subjective probabilities of success relative to effort, and success relative to ability, jointly and symmetrically. In this case, success would be instantiated once we can simultaneously overcome the difficulty relative to effort AND the difficulty relative to ability. To incorporate this parametrically in the model I have relied on a tool called a copula function, which describes algebraically the form of dependence between the task difficulty (or equivalently probability of success) relative to ability and effort.
Specifically, I use a Frank copula (Figure 6), which allows for a flexible symmetrical structure without imposing limits on the tail correlations, where:


The resultant motivational profile based on the psychologically constitutive adjustments to Figure 5 in the presence of a growth mindset is shown in the dynamic 'cobra-hooded' Figure 7 below. What is interesting to note is that while the uplift in overall motivation compared to a fixed mindset is evident, there are regions corresponding to easier task profiles for which one may actually be less motivated in adopting a growth mindset. This might occur in practice if the shift in ZPD is not properly accounted for to commensurately challenge competency activities. Additionally, accounting for ability as a resource may crowd-out effort, or allow for other essentialised attributions to present more conspicuously. Such feedback properties can be modelled using other varieties of copula dependency functions.
Fig. 7 -Sigmoid Achievement Motivation under Growth Mindset - Ability as a Resource
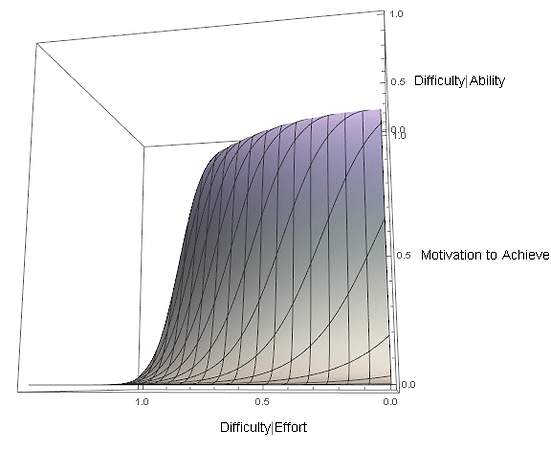
These analyses show the great potential for modelling psychological phenomenon, alongside established empirical rationales. Furthermore, it should be clear that while the architecture of a growth mindset can substantially transform one's motivational profile for competence under certain task regimes, by no means should it be treated as an ultimate panacea to problems, until the theoretical benefits have been well defined.
Cite this resource:
Jogie, M.R., (2019, June). Thinking Mindsets: Advancing Analytics. Retrieved from https://www.melissajogie.com/3d-growth-mindset